Labyrinthes

par · Publié · Mis à jour

Définitions

Un labyrinthe est une surface connexe. De telles surfaces peuvent avoir des topologies différentes : simple, ou comportant des anneaux ou des îlots.

On peut distinguer deux catégories de labyrinthe :

  • les labyrinthes « parfaits » : chaque cellule est reliée à toutes les autres et, ce, de manière unique.

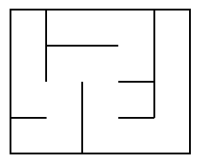
  • les labyrinthes « imparfaits » (tous les labyrinthes qui ne sont pas parfaits) : ils peuvent donc contenir des boucles, des îlots ou des cellules inaccessibles.

Pour la suite, nous choisissons de représenter un labyrinthe par un graphe, dont les sommets représentent des cellules (tuples de coordonnées (ligne, colonne)) et les arêtes des passages entre deux cellules (l’absence d’arête équivaut alors à un mur).

 

Activité : graphe d'un labyrinthe
Dessiner le labyrinthe défini par le graphe ci-dessous.
lab1 = {(0,0):{(0,1),(1,0)}, (0,1):{(0,0),(1,1)},(0,2):{(1,2),(0,3)},(0,3):{(0,2),(1,3)},(1,0):{(0,0),(2,0)},(1,1):{(0,1),(1,2)},(1,2):{(1,1),(0,2)},(1,3):{(0,3),(2,3)},(2,0):{(1,0),(2,1)},(2,1):{(2,0)},(2,2):{(2,3),(3,2)},(2,3):{(1,3),(2,2),(3,3)},(3,0):{(3,1),(4,0)},(3,1):{(3,0),(3,2)},(3,2):{(3,1),(2,2)},(3,3):{(2,3)},(4,0):{(3,0),(4,1)},(4,1):{(4,0),(4,2)},(4,2):{(4,1),(4,3)},(4,3):{(4,2)}}
Implémenter une instance de Labyrinthe pour représenter le labyrinthe ci-dessous sous la forme d'un graphe (par dictionnaire d'adjacence Python).

 

Implémentation

Nous définissons une classe Labyrinthe, héritant d’une classe Graphe, et munie d’une méthode de représentation en mode semi-graphique (avec des caractères spéciaux).

Classe Labyrinthe
class Labyrinthe(Graphe):
    #        0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
    #coins = [" ", "╶", "╵", "└", "╴", "─", "┘", "┴", "╷", "┌", "│", "├", "┐", "┬", "┤", "┼"]
    coins = [" ", "═", "║", "╚", "═", "═", "╝", "╩", "║", "╔", "║", "╠", "╗", "╦", "╣", "╬"]
    #coins = [" ", "█", "█", "█", "█", "█", "█", "█", "█", "█", "█", "█", "█", "█", "█", "█"]

    def __init__(self, w = 0, h = 0):
        Graphe.__init__(self, oriente = False)

        self.w = w
        self.h = h
        self.reset()

        # Tableau de la représentation du labyrinthe en mode semi-graphique
        self.repr = [["*"]*(2*self.w+1) for c in range(2*self.h+1)]
        self.effacer_repr()

        # Coordonnées des ouvertures vers l’extérieur
        self.ouvertures = []
        

    def reset(self):
        self.A = {}
        for l in range(self.h):
            for c in range(self.w):
                self.ajouter_sommet((l, c))


    ##################################################################################
    ### méthodes pour représentation
    ##################################################################################
    def __repr__(self):
        self.construire_repr()
        L = []
        for l in self.repr:
            L.append("".join(l))
        return "\n".join(L)


    def construire_repr(self):
        """ Construit la représentation du labyrinthe en mode semi-graphique
            dans le tableau à deux dimensions self.repr
            self.ouvertures : liste des ouvertures vers l'extérieur (cellules : tuple (l,c))
        """
        # Les murs
        for c in range(self.w):
            self.repr[0][2*c+1] = Labyrinthe.coins[5]
        for l in range(self.h):
            self.repr[2*l+1][0] = Labyrinthe.coins[10]
            for c in range(self.w):
                if l+1 < self.h and self.arete((l, c), (l+1, c)):
                    self.repr[2*l+2][2*c+1] = Labyrinthe.coins[0]
                else:
                    self.repr[2*l+2][2*c+1] = Labyrinthe.coins[5]

                if c+1 < self.w and self.arete((l, c), (l, c+1)):
                    self.repr[2*l+1][2*c+2] = Labyrinthe.coins[0]
                else:
                    self.repr[2*l+1][2*c+2] = Labyrinthe.coins[10]

        # Les coins
        for l in range(0, len(self.repr), 2):
            for c in range(0, len(self.repr[0]), 2):
                code  = 1 * (c+1 < len(self.repr[0]) and self.repr[l][c+1] != " ")
                code += 2 * (l != 0 and self.repr[l-1][c] != " ")
                code += 4 * (c != 0 and self.repr[l][c-1] != " ")
                code += 8 * (l+1 < len(self.repr) and self.repr[l+1][c] != " ")
                self.repr[l][c] = Labyrinthe.coins[code]

        # Les ouvertures vers l’extérieur
        for o in self.ouvertures:
            l, c = o
            if c == 0:
                self.repr[2*l+1][2*c] = " "
            elif c == self.w-1:
                self.repr[2*l+1][2*c+2] = " "
            elif l == 0:
                self.repr[2*l][2*c+1] = " "
            elif l == self.h-1:
                self.repr[2*l+2][2*c+1] = " "


    def effacer_repr(self):
        for l in range(self.h):
            for c in range(self.w):
                self.repr[2*l+1][2*c+1] = " "
Classe Graphe
class Graphe:
    """ Implémentation d'un graphe à partir d'un dictionnaire d'adjacence
    """
    def __init__(self, oriente = True):
        self.A = {}
        self.oriente = oriente

    def __repr__(self):
        return str(self.A)

    def __len__(self):
        return len(self.A)

    def construire(self, A):
        """ Construit le graphe à partir d'un dictionnaire d'adjacence
        """
        self.w = self.h = 0
        self.A = A
        for s in A:
            self.w = max(self.w, s[1]+1)
            self.h = max(self.h, s[0]+1)

    def ajouter_sommet(self, x):
        """ Ajoute un sommet x
        """
        if not x in self.A:
            self.A[x] = set()

    def ajouter_arete(self, x, y):
        """ Ajoute une arête entre les sommets x et y
        """
        self.ajouter_sommet(x)
        self.ajouter_sommet(y)
        self.A[x].add(y)
        if not self.oriente:
            self.A[y].add(x)

    def voisins(self, x):
        """ Renvoie l'ensemble des voisins du sommet x
        """
        return self.A[x]

    def aretes(self):
        """ Renvoie la liste de toutes les arêtes du graphe
        """
        for x, V in self.A.items():
            for v in V:
                L.append((x, v))
        return L

    def arete(self, x, y):
        """ Renvoie True s'il existe une arête
            entre le sommet x et le sommet y
        """
        return x in self.A[y]

    ############################################################################
    # Profondeur
    ############################################################################
    def parcours_prof(self, s, vus = set()):
        """ Parcours en profondeur à partir du sommet s
            --> renvoie vus : ensemble des sommets visités
            (fonction récursive)
        """
        if not s in vus:
            vus.add(s)
            for v in self.voisins(s):
                self.parcours_prof(v, vus)
        return vus


    def parcours_ch(self, s, ori = None, vus = set()):
        """ Parcours en profondeur à partir du sommet s
            en venant de ori
        """
        if not s in vus:
            vus[s] = ori
            for v in self.voisins(s):
                self.parcours_ch(v, s, vus)
        return vus


    def chemins(self, x, y):
        """ Parcours en profondeur à partir du sommet s
            Renvoie la liste des chemins parcourus
        """
        vus = self.parcours_ch(x)
        c = []
        if y in vus:
            s = y
            while s is not None:
                c.append(s)
                s = vus[s]
        return c[::-1]


    def existe_chemin(self, x, y):
        """ Renvoie True si un chemin existe entre les sommets x et y
        """
        return y in self.parcours_prof(x)



    ############################################################################
    # Largeur
    ############################################################################
    def parcours_larg(self, s):
        """ Parcours en largeur du graphe, à partir du sommet s
        """
        dist = {s : 0}
        cour = {s}
        suiv = set()
        while len(cour) > 0:
            s = cour.pop()
            for v in self.voisins(s):
                if not v in dist:
                    suiv.add(v)
                    dist[v] = dist[s] + 1
            if len(cour) == 0:
                cour, suiv = suiv, set()
        return dist


    def parcours_larg_chemin(self, s):
        """ Parcours en largeur du graphe, à partir du sommet s
            Renvoie un dictionnaire {sommet: précédent}
            qui doit permettre de construire des chemins depuis A
        """
        vus = {s : None}
        cour = {s}
        suiv = set()
        while len(cour) > 0:
            s = cour.pop()
            for v in self.voisins(s):
                if not v in vus:
                    suiv.add(v)
                    vus[v] = s
            if len(cour) == 0:
                cour, suiv = suiv, set()
        return vus


    def chemins_larg(self, x, y):
        """ Parcours en profondeur à partir du sommet s
            Renvoie la liste des chemins parcourus
        """
        vus = self.parcours_larg_chemin(x)
        c = []
        if y in vus:
            s = y
            while s is not None:
                c.append(s)
                s = vus[s]

        return c[::-1]


    def distance(self, x, y):
        dist = parcours_larg(x)
        return dist[v] if v in dist else None

 

Quelques méthodes pour Labyrinthe ...
Ajouter deux méthodes murs_cellule(s) et voisins_cellule(s) qui renvoient respectivement la liste des murs adjacents à la cellule s , ouvert (passage) ou pas, et la liste des cellules voisines de la cellule s , accessibles ou pas.

 

On souhaite pouvoir instancier un labyrinthe déjà défini par son dictionnaire d'adjacence.

Modifier la méthode de construction du labyrinthe pour rendre cela possible (on utilisera un paramètre à mot clé supplémentaire A = None).

 

Ajouter une méthode ouvrir_passage(x, y) permettant d'ouvrir un passage entre les cellules x et y. Cette méthode doit utiliser la méthode Graphe.ajouter_arete, et doit vérifier que xet y sont bien deux cellules adjacentes.

 

 

Construction d’un labyrinthe

Il existe de très nombreux algorithmes de construction de labyrinthe…

Fusion aléatoire de chemins

  • On part d’un labyrinthe dont tous les murs sont fermés,
  • On associe une valeur unique (un identifiant) à chaque cellule,
  • À chaque itération, on choisit un mur à ouvrir de manière aléatoire,
  • Lorsqu’un mur est ouvert entre deux cellules adjacentes, les deux cellules sont liées entre elles et forment un « chemin ».
  • À chaque fois que l’on tente d’ouvrir un passage entre deux cellules, on vérifie que ces deux cellules ont des identifiants différents.
    • Si les identifiants sont identiques, c’est que les deux cellules sont déjà reliées et appartiennent donc au même chemin. On ne peut donc pas ouvrir le passage.
    • Si les identifiants sont différents, le passage est ouvert, et l’identifiant de la première cellule est affecté à toutes les cellules du second chemin.

Construction d'un graphe par fusion de chemins
Implémenter cet algorithme dans une méthode construire_fusion().

 

Algorithme de Prim

On part d’un labyrinthe dont tous les murs sont fermés.

On crée :

  • une liste de cellules « non visitées » (pleine au départ)
  • une liste de murs (initialement les murs adjacents d’une cellule choisie aléatoirement)

Tant qu’il y a des murs dans la liste :

  • on choisit un mur au hasard dans la liste.
  • si une seule des deux cellules que le mur divise est visitée, alors :
    • on ouvre un passage à travers ce mur
    • on marque la cellule « non visitée » comme « visitée » (on la supprime de la liste)
    • on ajoute les murs voisins de la cellule à la liste des murs.
  • on retire le mur de la liste.

 

Construction d'un graphe par l'algorithme de Prim
Implémenter cet algorithme dans une méthode construire_prim().

 

Version modifiée

Bien que l’algorithme classique de Prim conserve une liste de bords, pour la génération de labyrinthes, nous pourrions plutôt maintenir une liste de cellules adjacentes. Si la cellule choisie au hasard comporte plusieurs bords qui la relient au labyrinthe existant, sélectionnez l’un de ces bords au hasard. Cela aura tendance à créer des branches légèrement plus nombreuses que la version basée sur les bords ci-dessus.

 

Algorithme d’Aldous-Broder

  • On choisit une cellule au hasard comme « cellule courante » et on la marque comme « visitée ».
  • Tant qu’il existe des cellules non visitées :
    • On choisit un voisin au hasard,
    • Si le voisin choisi n’a pas encore été visité :
      • On ouvre un passage entre la « cellule courante » et le voisin choisi,
      • On marque le voisin choisi comme étant visité,
    • On fait du voisin choisi la « cellule courante ».

Construction d'un graphe par l'algorithme d'Aldous-Broder
Implémenter cet algorithme dans une méthode construire_aldous_broder().

Pour en savoir plus …
https://weblog.jamisbuck.org/2011/1/17/maze-generation-aldous-broder-algorithm

 

Division récursive

  • On part d’un labyrinthe sans aucun mur.
  • On définit une « chambre » (rectangle interne au labyrinthe), initialement égale au labyrinthe entier.
    • On coupe cette chambre en deux parties (de tailles égales ou aléatoirement) en construisant un mur (vertical ou horizontal – alternativement ou aléatoirement)
    • On ouvre un passage au hasard dans ce grand mur
    • On recommence avec les deux chambres
  • La récursion s’arrête lorsqu’on ne peut plus couper la chambre en deux parties, au moins dans une direction.

Construction d'un graphe par l'algorithme de division
Implémenter cet algorithme dans une méthode construire_division().
Un peu d'aide
Voici un schéma illustrant une chambre (l, c, w, h) et une séparation horizontale (après la colonne mc), générant alors deux nouvelles chambres … dont il faut déterminer les dimensions … et ensuite diviser.

 

 

Autres algorithmes

Wilson

https://weblog.jamisbuck.org/2011/1/20/maze-generation-wilson-s-algorithm.html

 

Hunt and kill

https://weblog.jamisbuck.org/2011/1/24/maze-generation-hunt-and-kill-algorithm.html

 

Résolution

À présent qu’un labyrinthe parfait est construit, il faut y jouer ! Pour cela on peut par exemple demander au joueur de trouver la sortie.

On souhaite proposer au joueur de sortir du labyrinthe (cellule située sur un bord) à partir d’une cellule de départ (également située sur un bord).

Le plus court chemin pour sortir devra être le plus long chemin existant entre deux cellules du bord du labyrinthe. Reste à déterminer quelles sont ces deux cellules…

Les bords
Écrire une méthode bords de la classe Labyrinthe qui renvoie la liste de toutes les cellules du bord.

 

Le labyrinthe étant structurellement un graphe, on peut facilement y déterminer des chemins, en utilisant un parcours en largeur (voir recherche de chemins).

Pour visualiser le résultat, on peut utiliser la méthode suivante qui enrichie la méthode de représentation __repr__.

def remplir_chemin(self, lst):
    """ Trace le chemin constitué d'une liste de cellules (lst)
        avec des numéros d'indice (dernier chiffre)
    """
    i = 0
    for s in lst:
        l, c = s
        self.repr[2*l+1][2*c+1] = str(i)[-1]
        i += 1

 

Plus long chemin
Écrire une méthode plus_long_chemin_bords de la classe Labyrinthe qui renvoie le plus long chemin d'une cellule du bord à une autre.

 

Jeu-démo en ligne

Voici un petit jeu-démo réalisé en Javascript par les élèves de terminales 2020-2021 : https://blaisepascal.fr/labyrinthe/

 

Sources :
https://fr.wikipedia.org/wiki/Mod%C3%A9lisation_math%C3%A9matique_de_labyrinthe
https://en.wikipedia.org/wiki/Maze_generation_algorithm

Vous aimerez aussi...

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *